Making Icebergs for ICEBERG Package in MITgcm
This script generates random icebergs accoring to a power distribution, following (Davison et al. 2020) (10.5194/tc-16-1181-2022) and creates all accessory files needed to run MITgcm with this distribution of icebergs and desired custom masks. Last update November 2024. Please reach out for more up to date versions.
Loading libraries and establishing some helper functions
import numpy as np
import matplotlib.pyplot as plt
import fileinput
import sys
import cmocean
writeFiles = False # make True if want to actually save files
def setUpPrint(fname): #this functions lets you control how setup output is printed or saved.
print(fname)
def write_bin(fname, data):
setUpPrint(fname + str(np.shape(data)))
if(writeFiles):
data.astype(">f8").tofile(fname)
else:
setUpPrint('\tNot saving')
Make domain sizes, establish grid spacing
This must agree with dimensions from SIZE.h and input/data file
setUpPrint('====== Making mélange =====')
#Make Masks
nz = 50
ny = 12
nx = 40
# All meters
deltaZ = 10
deltaY = 500
deltaX = 500
dz = np.ones(nz) * deltaZ
iceBergDepth = 200 #[m]
iceExtent = 8000 #[m]
iceCoverage = 95 # Coverage of ice [%]
====== Making mélange =====
Make masks for customized behavior of icebergs
bergMask = 1 in all locations within the grid where icebergs may exist.
driftMask = 1 in all locations within the grid where iceberg melt velocities are calculated with respect to the average ocean current along the draft of the iceberg. This simulates drifting within the cell, but does not let the icebergs drift between cells. This should be =0 if bergs are locked within a mélange pack.
meltMask = 1 in all locations within the grid where iceberg melt is calculated. Without melt, bergs will only have a physical blocking interaction with the ocean, but no melt water or thermodynamic effect will be calculated.
barrierMask = 1 in all locations within the grid where the physical blocking effect of the icebergs will interact with the ocean.
bergConc is the percent surface area of ice at every gird cell with icebergs. To have 95% ice, input 95, not 0.95.
bergMaskNums is the assigned ID numbers of all grid cells with icebergs. This is assigned further below.
numBergsPerCell is the number of icebergs within every cell. This is populated further below.
bergMask = np.zeros([ny,nx])
driftMask = np.zeros([ny,nx])
meltMask = np.zeros([ny,nx])
barrierMask = np.zeros([ny,nx])
bergConc = np.zeros([ny,nx])
bergMaskNums = np.zeros([ny,nx])
numBergsPerCell = np.zeros([ny,nx],dtype=np.int64)
Set Parameters
Masks are populated here, and default iceberg parameters are input. These values can still adjustable as needed, but for simple cases can be left as default. At the end we output total area of grid to be filled with icebergs, total top surface area of icebergs, and the ratio as a sanity check. This should equal the bergConc if bergConc is uniform for iceberg cells.
# Berg parameters
bergType = 1 # 1 = block 2 = cone (not implemented)
alpha = 1.8 # slope of inverse power law size frequency distribution
scaling = 2 # 1 = Sulak 2017 2 = Barker 2004
maxBergDepth = iceBergDepth # (m) - set to zero if 'prescribing' max iceberg width, set at top here
minBergDepth= 20 # (m)
maxBergWidth = 0 # (m) - set to zero if 'prescribing' max iceberg depth
minBergWidth = 20 # (m)
if(scaling == 1): # then use Sulak17 volume-area scaling volume = 6.0*area^1.30
# assumes volume = L*W*D and W = L/1.62 (Dowdeswell et al 1992)
if(maxBergWidth==0):
maxBergWidth = 0.0642449*maxBergDepth**(5/3)
# minBergWidth = 0.0642449*minBergDepth**(5/3)
elif(maxBergDepth==0):
maxBergDepth = 5.19155*maxBergWidth**(5/3)
minBergDepth = 5.19155*minBergWidth**(5/3)
elif(scaling == 2): # Then use Barker04 width-depth relationship
# Depth = 2.91*Width^0.71
if(maxBergWidth==0):
maxBergWidth = (100*10**(58/71)*maxBergDepth**(100/71)) / (291*291**(29/71))
#minBergWidth = (100*10**(58/71)*minBergDepth**(100/71)) / (291*291**(29/71))
elif(maxBergDepth==0):
maxBergDepth = 2.91*maxBergWidth^0.71
minBergDepth = 2.91*minBergWidth^0.71
#Extent of ice in grid cells
iceExtentIndex = int(np.round(iceExtent/deltaX))
# Iceberg mask
bergMask[1:-1,1:iceExtentIndex] = 1 # icebergs, all oriented east-west (other values can turn bergs, PS has not tested this functionality)
# Drift mask, No drift for Melange experiments, but can toggle on here if you want
# driftMask[1:-1,1:iceExtentIndex] = 1 # calculate effect of iceberg drift on melt rates
# Melt mask, only let bergs melt in this region (make melt water, these don't change size)
meltMask[1:-1,1:iceExtentIndex] = 1 # Allow focus on blocking effect only
# Barrier mask
barrierMask[1:-1,1:iceExtentIndex] = 1 # make icebergs a physical barrier to water flow
# Iceberg concentration (# of each surface cell that is filled in plan view)
bergConc[1:-1,1:iceExtentIndex] = iceCoverage # iceberg concentration set at top
desiredBergArea = np.sum(bergConc/100.0*deltaX*deltaY)
bergMaskArea = np.sum(bergMask*deltaX*deltaY)
setUpPrint('Area where bergs live: ' + str(bergMaskArea) + ' m^2')
setUpPrint('Desired berg area: ' + str(desiredBergArea) + ' m^2')
setUpPrint('Ratio: ' + str(desiredBergArea/bergMaskArea*100) + '%') #This should equal the bergConc if uniform for iceberg cells.
Area where bergs live: 37500000.0 m^2
Desired berg area: 35625000.0 m^2
Ratio: 95.0%
Generating Icebergs
Now the fun. This section generates icebergs from a power distribution and compares the total top surface area of the bergs to the desired area of bergs. This is a random process, so it may bounce around a few times before reaching the match criteria. Bergs are clipped horizontally so they fit into one cell for simplicity, this is a deviation from the method of Davison et al who split large bergs into multiple cells. Progress is printed, and exit condition printed.
numberOfBergs = 1000 #low start, immediately doubled by scheme below, so guess low, high guesses (300%+) can cause to fail
bergTopArea = 0
areaResidual = 1
# Generate the Inverse Power Law cumulative distribution function
# over the range minBergWidth-maxBergWidth with a slope of alpha.
setUpPrint('Making bergs, this can take a few loops...')
loop_count = 1
while(np.abs(areaResidual) > .03 ): # Ensure correct surface area, I set to .01 for more exact coverage, but longer generation time
numberOfBergs = round(numberOfBergs * (1 + areaResidual))
setUpPrint('\tnumberOfBergs: ' + str(numberOfBergs))
x_width = np.arange(minBergWidth, maxBergWidth, (maxBergWidth-minBergWidth)/(numberOfBergs*1e2))
x_depth = np.arange(minBergDepth, maxBergDepth, (maxBergDepth-minBergDepth)/(numberOfBergs*1e2))
inversePowerLawPDF_width = ((alpha-1) / minBergWidth) * (x_width/minBergWidth) ** (-alpha)
inversePowerLawPDF_depth = ((alpha-1) / minBergDepth) * (x_depth/minBergDepth) ** (-alpha)
# Get the CDF numerically
inversePowerLawCDF_width = np.cumsum(inversePowerLawPDF_width)
inversePowerLawCDF_depth = np.cumsum(inversePowerLawPDF_depth)
# Normalize
inversePowerLawCDF_width = inversePowerLawCDF_width / inversePowerLawCDF_width[-1]
inversePowerLawCDF_depth = inversePowerLawCDF_depth / inversePowerLawCDF_depth[-1]
# Generate number_of_bergs uniformly distributed random numbers.
uniformlyDistributedRandomNumbers = np.random.uniform(0,1,numberOfBergs)
inversePowerLawDistNumbers_width = np.zeros(uniformlyDistributedRandomNumbers.size);
inversePowerLawDistNumbers_depth = np.zeros(uniformlyDistributedRandomNumbers.size);
nearestIndex_width = [0] * uniformlyDistributedRandomNumbers.size
nearestIndex_depth = [0] * uniformlyDistributedRandomNumbers.size
for i in range(uniformlyDistributedRandomNumbers.size): #this is pretty slow, not sure if vectorized exists
nearestIndex_width[i] = np.abs(uniformlyDistributedRandomNumbers[i]-inversePowerLawCDF_width).argmin();
nearestIndex_depth[i] = np.abs(uniformlyDistributedRandomNumbers[i]-inversePowerLawCDF_depth).argmin();
inversePowerLawDistNumbers_width = x_width[nearestIndex_width];
inversePowerLawDistNumbers_length = inversePowerLawDistNumbers_width/1.62 # Widths are bigger
tooWide = np.count_nonzero(inversePowerLawDistNumbers_width > deltaX)
tooLong = np.count_nonzero(inversePowerLawDistNumbers_width > deltaX)
inversePowerLawDistNumbers_width[inversePowerLawDistNumbers_width > deltaX] = deltaX # Max width is grid cell (assumed square)
inversePowerLawDistNumbers_length[inversePowerLawDistNumbers_length > deltaX] = deltaX # Max length is grid cell (assumed square)
if(tooLong + tooWide > 0):
setUpPrint('\t\tBergs clipped: %i for width, %i for length' % (tooWide, tooLong))
inversePowerLawDistNumbers_depth = x_depth[nearestIndex_depth]; #depths don't get clipped
bergTopArea = sum(inversePowerLawDistNumbers_width*inversePowerLawDistNumbers_length)
areaResidual = (desiredBergArea - bergTopArea)/desiredBergArea
setUpPrint('\t\t%.2f %% Bergs' % (bergTopArea/bergMaskArea*100))
setUpPrint('\t\tareaResidual %.2f %%' % (areaResidual * 100))
loop_count += 1
setUpPrint('====== Success! Found our bergs =====')
setUpPrint('Width min/mean/max: %f/%f/%f [m]' % (np.min(inversePowerLawDistNumbers_width),np.mean(inversePowerLawDistNumbers_width),np.max(inversePowerLawDistNumbers_width)))
setUpPrint('Depth min/mean/max: %f/%f/%f [m]' % (np.min(inversePowerLawDistNumbers_depth),np.max(inversePowerLawDistNumbers_depth),np.max(inversePowerLawDistNumbers_depth)))
setUpPrint('Total Berg Area %f' % bergTopArea)
setUpPrint('Total Berg fract: %.2f %%' % (bergTopArea/bergMaskArea*100))
Making bergs, this can take a few loops...
numberOfBergs: 2000
32.73 % Bergs
areaResidual 65.54 %
numberOfBergs: 3311
55.61 % Bergs
areaResidual 41.46 %
numberOfBergs: 4684
77.72 % Bergs
areaResidual 18.19 %
numberOfBergs: 5536
93.18 % Bergs
areaResidual 1.91 %
====== Success! Found our bergs =====
Width min/mean/max: 20.001988/72.124486/386.819828 [m]
Depth min/mean/max: 20.001951/199.997724/199.997724 [m]
Total Berg Area 34944156.928792
Total Berg fract: 93.18 %
Placing Icebergs
After icebergs are generated, they are sorted large to small, then placed into random cells 1 at a time. Large bergs are placed first to ensure no berg is left unplaced. When cells are too full for the currently being placed cell, another random cell is picked until the berg fits. Further can bergs can still be placed into that cell until it reaches the full criteria (2% more than bergConc). This method tends to generate many cells at the full criteria. Loosening the full critera (higher pad) could allow a more uniform distribution of ice berg concentration across all cells, but here this is optimized for high iceberg concentration (~95%) and so a cap below 100% was selected.
# Now we sort these berg into cell, randomly
bergMaski = 0 #Bad name, but this is the count of cells that will recieve bergs
bergDict = {}
for j in range(ny):
for i in range(nx):
if(bergMask[j,i] == 1):
# print('i,j, bergmask',i,j,bergMask[j,i])
bergMaski = 1 + bergMaski #Needs to start at 1, as non-bergs will be 0
bergMaskNums[j,i] = bergMaski #Assign Mask Nums, not random as we'll randomly place bergs in cells
bergDict[bergMaski] = [j,i] #This lets us do 1-D loops for the whole grid
setUpPrint('%i cells with bergs' % bergMaski)
# print(bergDict)
# Sort my bergs
sorted_indices = np.argsort(-inversePowerLawDistNumbers_depth) # Sort backwards to get descending from big to small bergs
sorted_depth = inversePowerLawDistNumbers_depth[sorted_indices]
sorted_width = inversePowerLawDistNumbers_width[sorted_indices]
sorted_length = inversePowerLawDistNumbers_length[sorted_indices]
assignedCell = np.random.randint(0,bergMaski,[numberOfBergs]) # In this script, every berg has a home
# Need to reshuffle as it re-writes this when sorting
# Array for bergs
bergsPerCellLimit = 500
icebergs_depths = np.zeros([bergMaski,bergsPerCellLimit])
icebergs_widths = np.zeros([bergMaski,bergsPerCellLimit])
icebergs_length = np.zeros([bergMaski,bergsPerCellLimit]) #careful, not plural as to length match
assignedCell = np.random.randint(0,bergMaski,[numberOfBergs]) #every Berg has a spot
icebergs_per_cell = np.zeros([bergMaski],dtype=np.int16)
icebergs_area_per_cell = np.zeros([bergMaski])
for i in range(numberOfBergs):
j = assignedCell[i]
# print('looking at mask number',j,'at berg',i)
# print('Berg number', icebergs_per_cell[j],'in this cell')
bergArea = sorted_width[i] * sorted_length[i]
loopLimiter = 0
while(bergArea > (deltaX * deltaY * (bergConc[bergDict[j+1][0],bergDict[j+1][1]]/100 + .02) - icebergs_area_per_cell[j])): #if too full, pick random new cell
j_old = j
j = np.random.randint(0,bergMaski)
assignedCell[i] = j
loopLimiter += 1
# print(j_old, "is full, trying",j, "attempt", loopLimiter)
if(loopLimiter > bergMaski):
setUpPrint('no more empty cells... giving up')
break
icebergs_depths[j,icebergs_per_cell[j]] = sorted_depth[i]
icebergs_widths[j,icebergs_per_cell[j]] = sorted_width[i]
icebergs_length[j,icebergs_per_cell[j]] = sorted_length[i]
icebergs_per_cell[j] += 1
# icebergs_area_per_cell[j] = np.sum(icebergs_widths[j,:]*icebergs_length[j,:])
icebergs_area_per_cell[j] += bergArea
# setUpPrint('Bergs per cell and filled faction at surface for spot check')
# setUpPrint(icebergs_per_cell)
# setUpPrint(np.round(icebergs_area_per_cell/(500*500),2))
# All bergs now sorted
openFrac = np.zeros([nz,ny,nx])
SA = np.zeros([nz,ny,nx])
SA[:,:,:] = np.nan
cellVolume = deltaX*deltaY*deltaZ
#This loop knows which cells should contain bergs are already, so we don't search for bergs across entire model domain
for i in range(bergMaski):
bergCount = icebergs_per_cell[i]
numBergsPerCell[bergDict[i+1][0],bergDict[i+1][1]] = bergCount
if(bergCount > 1):
lengths = icebergs_length[i,icebergs_length[i,:] > 0] #return only non-zeros
widths = icebergs_widths[i,icebergs_widths[i,:] > 0] #return only non-zeros
depths = icebergs_depths[i,icebergs_depths[i,:] > 0] #return only non-zeros
for k in range(nz):
d_bot = k*deltaZ + deltaZ #bottom of depth bin
d_top = k*deltaZ
volume1 = deltaZ * lengths[depths > d_bot] * widths[depths > d_bot]
SA1 = deltaZ*2*(lengths[depths > d_bot] + widths[depths > d_bot])
partialFill = (depths < d_bot) & (depths > d_top)
#partial fill
volume2 = (depths[partialFill] - d_top) * lengths[partialFill] * widths[partialFill]
#partial sides
SA2 = (depths[partialFill] - d_top)*2*(lengths[partialFill] + widths[partialFill])
#bottom
SA3 = lengths[partialFill] * widths[partialFill]
#print(np.sum(volume1), np.sum(volume2))
openFrac[k,bergDict[i+1][0],bergDict[i+1][1]] = 1-((np.sum(volume1) + np.sum(volume2))/cellVolume)
SA[k,bergDict[i+1][0],bergDict[i+1][1]] = np.sum(SA1) + np.sum(SA2) + np.sum(SA3)
elif(bergCount == 0):
openFrac[:,bergDict[i+1][0],bergDict[i+1][1]] = 1
SA[:,bergDict[i+1][0],bergDict[i+1][1]] = 0
150 cells with bergs
Plotting
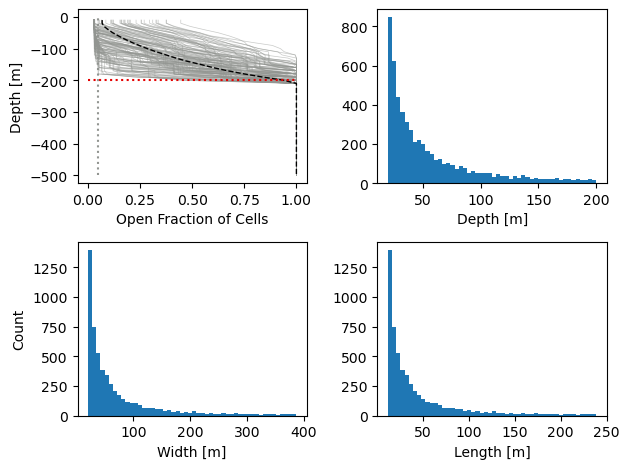
Output nice visuals of iceberg placement, depth distribution, and packing. These are also saved for later reference.
# Plots for reference on whats happening berg-wise
fig = plt.figure()
plt.subplot(2,2,1)
for i in range(bergMaski):
plt.plot(openFrac[:,bergDict[i+1][0],bergDict[i+1][1]],-np.cumsum(dz),alpha=.5,color='xkcd:gray',linewidth=.5)
plt.plot(np.mean(openFrac[:,bergMask==1],1),-np.cumsum(dz),alpha=1,color='xkcd:black',linewidth=1,linestyle='--',label='Average Bergs')
plt.plot([0,1],[-maxBergDepth,-maxBergDepth],color = 'xkcd:red',linestyle=':', label='Target Max Depth')
plt.plot([1-np.max(bergConc)/100,1-np.max(bergConc)/100],[-nz*deltaZ,0],color = 'xkcd:gray',linestyle=':',label='Target Max Berg Conc')
plt.xlabel('Open Fraction of Cells')
plt.ylabel('Depth [m]')
# plt.legend() #not quite room so off for now
plt.subplot(2,2,2)
plt.hist(inversePowerLawDistNumbers_depth,bins = 50)
# plt.ylabel('Count')
plt.xlabel('Depth [m]')
plt.subplot(2,2,3)
plt.hist(inversePowerLawDistNumbers_width,bins = 50)
plt.ylabel('Count')
plt.xlabel('Width [m]')
plt.subplot(2,2,4)
plt.hist(inversePowerLawDistNumbers_length,bins = 50)
# plt.ylabel('Count')
plt.xlabel('Length [m]')
fig.tight_layout()
plt.savefig('bergStatistics.png', format='png', dpi=200)
plt.show()
fig = plt.figure()
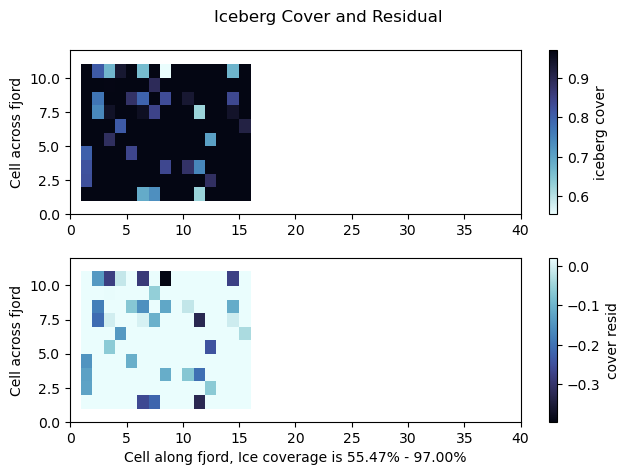
pltHelper = 1-openFrac[0,:,:]
pltHelper[bergMask == 0] = np.nan
plt.subplot(211)
pc = plt.pcolor(pltHelper,cmap='cmo.ice_r')
cbar = plt.colorbar(pc)
plt.suptitle('Iceberg Cover and Residual')
plt.ylabel('Cell across fjord')
cbar.set_label('iceberg cover')
plt.subplot(212)
pc = plt.pcolor(pltHelper - bergConc/100,cmap='cmo.ice')
cbar = plt.colorbar(pc)
pc_min = np.nanmin(pltHelper) * 100
pc_max = np.nanmax(pltHelper) * 100
plt.xlabel("Cell along fjord, Ice coverage is %.2f%% - %.2f%%" % (pc_min, pc_max))
plt.ylabel('Cell across fjord')
cbar.set_label('cover resid')
fig.tight_layout()
plt.savefig('bergMap.png', format='png', dpi=200)
plt.show()
fig = plt.figure()
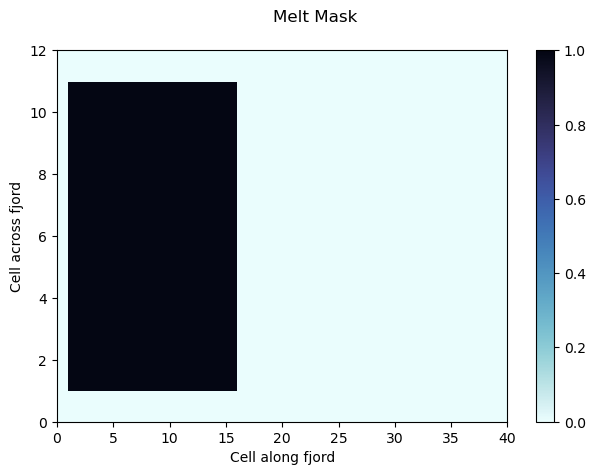
pc = plt.pcolor(meltMask,cmap='cmo.ice_r')
cbar = plt.colorbar(pc)
plt.suptitle('Melt Mask')
plt.ylabel('Cell across fjord')
plt.xlabel("Cell along fjord")
fig.tight_layout()
plt.savefig('meltMask.png', format='png', dpi=200)
plt.show()
/var/folders/56/63bb976d7mz5gryxtqfvqmgc0000gr/T/ipykernel_16172/217056070.py:36: MatplotlibDeprecationWarning: Getting the array from a PolyQuadMesh will return the full array in the future (uncompressed). To get this behavior now set the PolyQuadMesh with a 2D array .set_array(data2d).
cbar = plt.colorbar(pc)
/var/folders/56/63bb976d7mz5gryxtqfvqmgc0000gr/T/ipykernel_16172/217056070.py:43: MatplotlibDeprecationWarning: Getting the array from a PolyQuadMesh will return the full array in the future (uncompressed). To get this behavior now set the PolyQuadMesh with a 2D array .set_array(data2d).
cbar = plt.colorbar(pc)
Save output files
Now we save the files in various outputs. The iceberg_*.txt files are for compatability with the Davison et al (2020) verison of ICEBERG, and the icebergs_*.bin files are compatable with the new version of ICEBERG by Summers et al (2024) for this work. The presence of both file types doesn’t interfere with the function of either version of ICEBERG. The other .bin files are needed by both versions of ICEBERG. A final print message is printed at the very end.
# write iceberg txt files
setUpPrint('Saving text files for bergs...')
if(writeFiles):
for i in range(bergMaski):
with open('iceberg_depth_%05i.txt' % (i+1) , 'w') as file_handler:
for item in icebergs_depths[i,icebergs_depths[i,:] > 0]:
file_handler.write("{}\n".format(item))
with open('iceberg_width_%05i.txt' % (i+1) , 'w') as file_handler:
for item in icebergs_widths[i,icebergs_widths[i,:] > 0]:
file_handler.write("{}\n".format(item))
with open('iceberg_length_%05i.txt' % (i+1) , 'w') as file_handler:
for item in icebergs_length[i,icebergs_length[i,:] > 0]:
file_handler.write("{}\n".format(item))
icebergs_depths2D = np.zeros([bergsPerCellLimit,ny,nx])
icebergs_widths2D = np.zeros([bergsPerCellLimit,ny,nx])
icebergs_length2D = np.zeros([bergsPerCellLimit,ny,nx])
for k in range(bergMaski):
j = bergDict[k+1][0]
i = bergDict[k+1][1]
icebergs_depths2D[:,j,i] = icebergs_depths[k,:]
icebergs_widths2D[:,j,i] = icebergs_widths[k,:]
icebergs_length2D[:,j,i] = icebergs_length[k,:]
# write global files
write_bin('bergMask.bin',bergMask)
write_bin('bergMaskNums.bin',bergMaskNums)
write_bin('numBergsPerCell.bin',numBergsPerCell)
write_bin('openFrac.bin',openFrac)
write_bin('totalBergArea.bin',SA)
write_bin('meltMask.bin',meltMask)
write_bin('driftMask.bin',driftMask)
write_bin('barrierMask.bin',barrierMask)
write_bin('icebergs_depths.bin',icebergs_depths2D)
write_bin('icebergs_widths.bin',icebergs_widths2D)
write_bin('icebergs_length.bin',icebergs_length2D)
setUpPrint('Berg setup is done.')
Saving text files for bergs...
bergMask.bin(12, 40)
Not saving
bergMaskNums.bin(12, 40)
Not saving
numBergsPerCell.bin(12, 40)
Not saving
openFrac.bin(50, 12, 40)
Not saving
totalBergArea.bin(50, 12, 40)
Not saving
meltMask.bin(12, 40)
Not saving
driftMask.bin(12, 40)
Not saving
barrierMask.bin(12, 40)
Not saving
icebergs_depths.bin(500, 12, 40)
Not saving
icebergs_widths.bin(500, 12, 40)
Not saving
icebergs_length.bin(500, 12, 40)
Not saving
Berg setup is done.